Forces Acting on a Vehicle
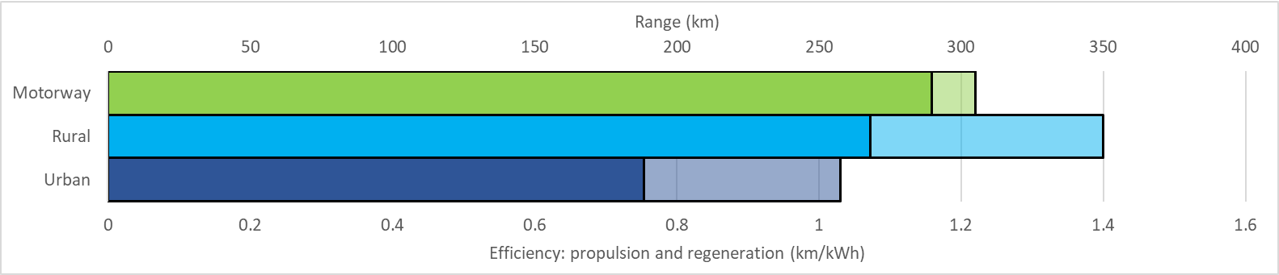
To understand these results, we dive deeper into the power requirements of each drive cycle to understand why relatively low speed urban driving requires more energy per km than higher speed motorway driving, and why rural driving is more efficient still.
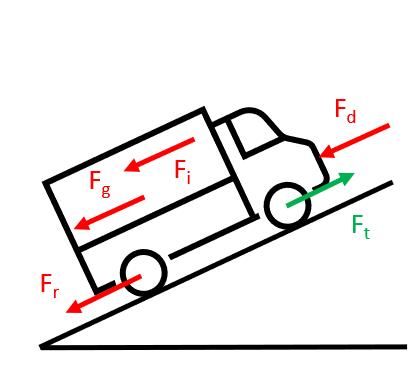 Power is required to deliver the tractive force (t) at the wheels to move the vehicle forward against opposing forces of:
Power is required to deliver the tractive force (t) at the wheels to move the vehicle forward against opposing forces of:
Inertia (i) (when accelerating)
Aerodynamic drag (d)
Rolling resistance of tyres (r)
Gravity (g) (when ascending a gradient)
The most important factors in power consumption of a vehicle are the speed and acceleration demanded by the driver, and the gradient of the road.
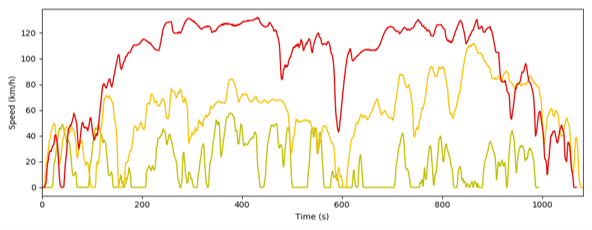
To help understand the reason for the different energy consumption for the three drive cycles, we calculate power curves. These show the instantaneous power required by the vehicle at specific speeds, accelerations and gradients.
These are created by isolating very short segments of telemetry data with a duration of less than 5 seconds (as illustrated above) during which the speed, acceleration and gradient are close to the values of interest. Many hundreds of such instances across all data for a vehicle are averaged to build the power curve.
Steady Speed
For this report we look only at the power requirements on flat roads. We start by looking at the power required at a constant speed. This is independent of payload, but will vary by factors such as wind, temperature and ancillary power loads.
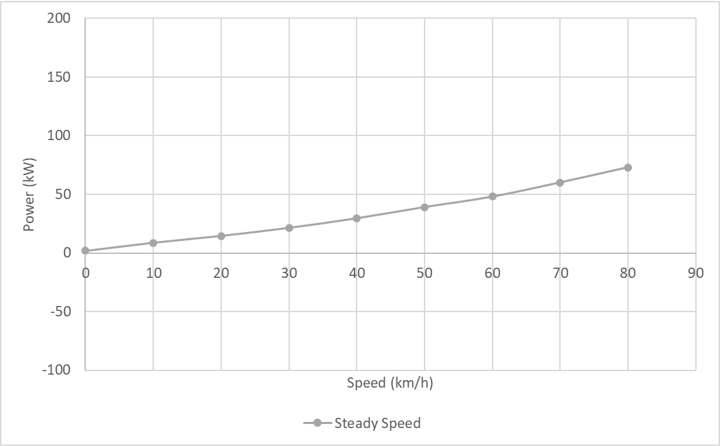 This graph shows the average power across all vehicles required to maintain a steady speed on the flat.
This graph shows the average power across all vehicles required to maintain a steady speed on the flat.
Typical urban speeds (30 to 50 km/h) require around 25 to 45 kW, maintaining the observed peak speed (80 km/h) requires around 70 kW.
Acceleration
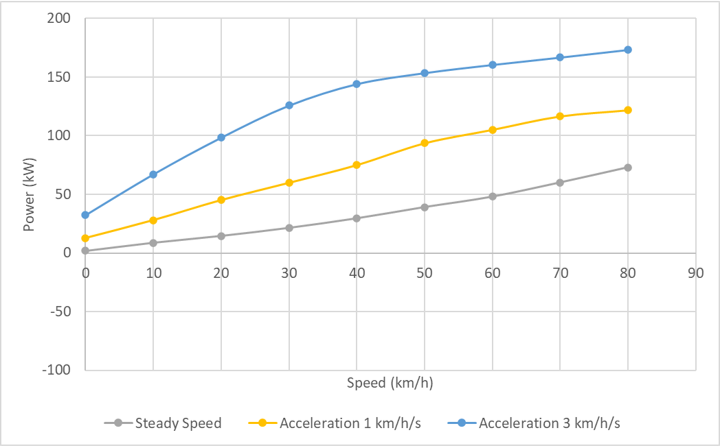 The power required to accelerate is, unsurprisingly, significantly higher, reaching above 150kW even at urban speeds. Higher acceleration rates and higher speeds require even more power.
The power required to accelerate is, unsurprisingly, significantly higher, reaching above 150kW even at urban speeds. Higher acceleration rates and higher speeds require even more power.
This analysis does not account for differing payload, which has a large impact on energy consumption when accelerating and decelerating.
It is possible that vehicles that reach higher speeds tend to be more lightly loaded, which would explain the flattening of the acceleration power curves at higher speeds.
The effects of payload will be analysed in future reports.
Deceleration
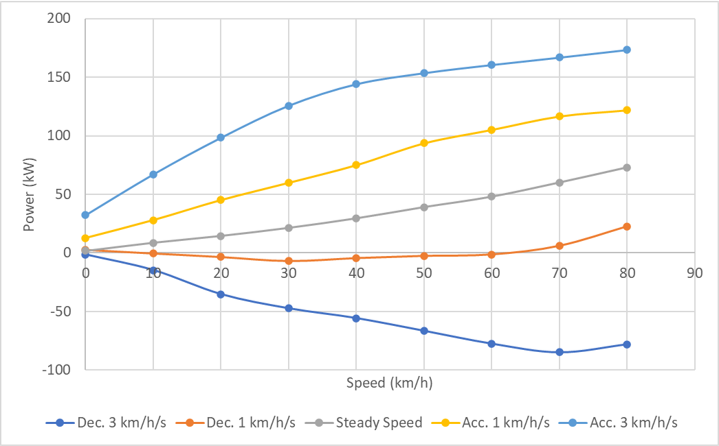 Adding in deceleration shows the power recovered from regeneration. At 1 km/h/s this is negligible because the vehicle will decelerate anyway due to air resistance, in fact at high speeds the drag is so great that power is still required during slow deceleration.
Adding in deceleration shows the power recovered from regeneration. At 1 km/h/s this is negligible because the vehicle will decelerate anyway due to air resistance, in fact at high speeds the drag is so great that power is still required during slow deceleration.
At 3 km/h/s deceleration, significant power is regenerated, but notably not as much as is required to accelerate the vehicle at the same rate. This is partly due to the capability of the motor-generator, but will also be affected by air resistance and the inevitable efficiency losses in the mechanical and electrical systems.
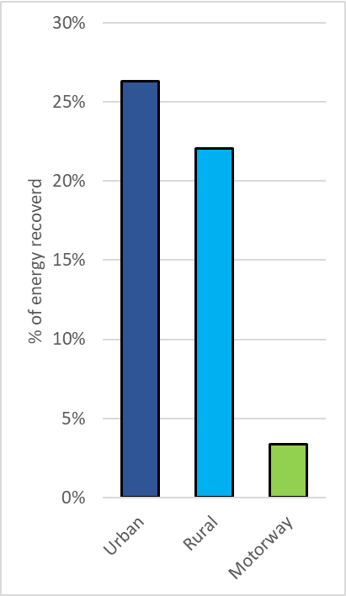
Regeneration power recovery at 3 km/h/s is about 30% to 50% of the propulsion power, depending on the speed.
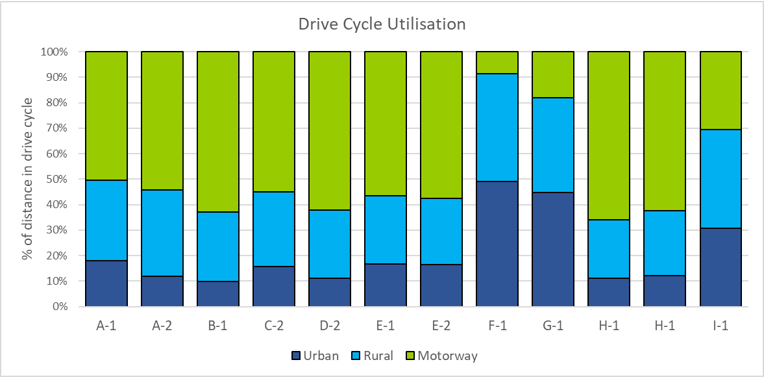
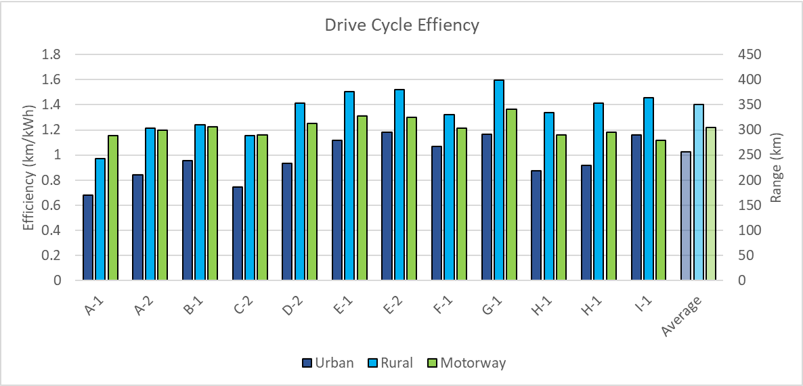
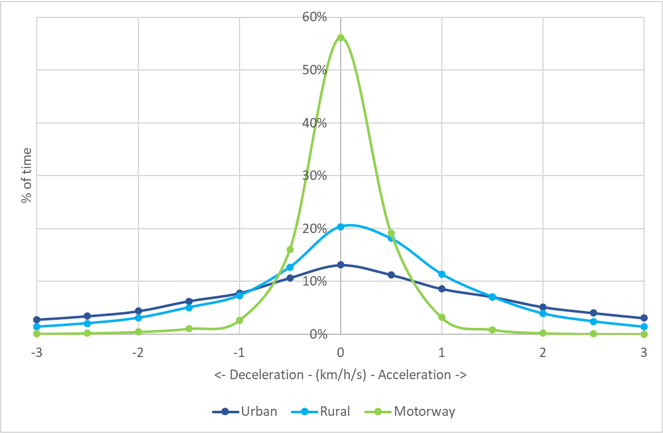 This graph shows the proportion of time spent at a steady speed and at various rates of acceleration and deceleration, for each drive cycle, averaged across all vehicles.
This graph shows the proportion of time spent at a steady speed and at various rates of acceleration and deceleration, for each drive cycle, averaged across all vehicles. Power is required to deliver the tractive force (t) at the wheels to move the vehicle forward against opposing forces of:
Power is required to deliver the tractive force (t) at the wheels to move the vehicle forward against opposing forces of: This graph shows the average power across all vehicles required to maintain a steady speed on the flat.
This graph shows the average power across all vehicles required to maintain a steady speed on the flat. The power required to accelerate is, unsurprisingly, significantly higher, reaching above 150kW even at urban speeds. Higher acceleration rates and higher speeds require even more power.
The power required to accelerate is, unsurprisingly, significantly higher, reaching above 150kW even at urban speeds. Higher acceleration rates and higher speeds require even more power. Adding in deceleration shows the power recovered from regeneration. At 1 km/h/s this is negligible because the vehicle will decelerate anyway due to air resistance, in fact at high speeds the drag is so great that power is still required during slow deceleration.
Adding in deceleration shows the power recovered from regeneration. At 1 km/h/s this is negligible because the vehicle will decelerate anyway due to air resistance, in fact at high speeds the drag is so great that power is still required during slow deceleration.